Ondas Ondulatorios

Ondas Ondulatorios!

Ondas Estacionarias en una Cuerda!
La formación de ondas estacionarias en una cuerda se debe a la suma (combinación lineal) de infinitos modos de vibración, llamados modos normales, los cuales tienen una frecuencia de vibración dada por la siguiente expresión (para un modo n):
f_n = \frac{nv}{2L}
Donde v es la velocidad de propagación, normalmente dada por v=\sqrt{\frac{T}{\mu}} para una cuerda de densidad \mu y tensión T.
La frecuencia más baja para la que se observan ondas estacionarias en una cuerda de longitud L es la que corresponde a n = 1 en la ecuación de los nodos (vista anteriormente), que representa la distancia máxima posible entre dos nodos de una longitud dada. Ésta se denomina frecuencia fundamental, y cuando la cuerda vibra de este modo no se presentan nodos intermedios entre sus dos extremos. La siguiente posibilidad en la ecuación, el caso n = 2, se llama segundo armónico, y presenta un nodo intermedio.\text{Si } x=L \text{ y } \lambda = \lambda_n \text{ entonces } L= n \cdot \frac{\lambda_n}{2} \qquad \text{ siendo } L \text{ la longitud de la cuerda dada}
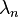despejamos \lambda_n:
  • \lambda_n = \frac{2L}{n}
Ondas Estacionarias De Un Tubo Abierto!


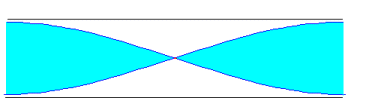
abierto1.gif (2864 bytes)
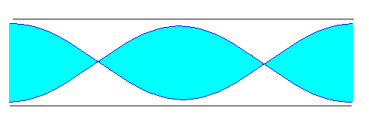
abierto2.gif (3171 bytes)
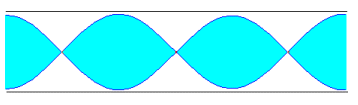abierto3.gif (3680 bytes)
Si un tubo es abierto, el aire vibra con su máxima amplitud en los extremos. En la figura, se representan los tres primeros modos de vibración
Como la distancia entre dos nodos o entre dos vientres es media longitud de onda. Si la longitud del tubo es L, tenemos que
L=l /2, L=l , L=3l /2, ... en general L=nl /2, n=1, 2, 3... es un número entero
Considerando que l =vs/f (velocidad del sonido dividido la frecuencia)
Las frecuencias de los distintos modos de vibración responden a la fórmula
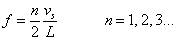Ondas Estacionarias En Un Tubo Cerrado!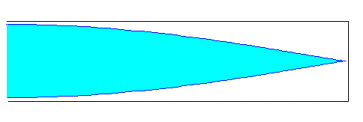
cerrado1.gif (2504 bytes)
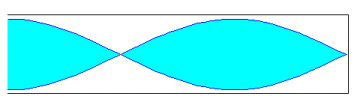
cerrado2.gif (2864 bytes)
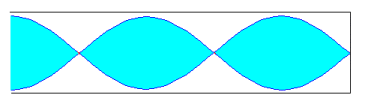cerrado3.gif (3342 bytes)
Si el tubo es cerrado se origina un vientre en el extremo por donde penetra el aire y un nodo en el extremo cerrado. Como la distancia entre un vientre y un nodo consecutivo es l /4. La longitud L del tubo es en las figuras representadas es L=l /4, L=3l /4, L=5l /4...
En general L=(2n+1) l /4; con n=0, 1, 2, 3, ...
Las frecuencias de los distintos modos de vibración responden a la fórmula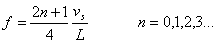

No hay comentarios:

Publicar un comentario

Suscribirse a: Entradas (Atom)